Sudoku Anleitung

Was ist Sudoku Anleitung? Die Geschichte der Sudokus haben wir in 3 wichtige Bereiche aufgeteilt. Zunächst werden wir auf den Ursprung der Sudokus in den magischen Quadraten eingehen. Im zweiten Teil zeigen wir den Übergang der klassischen Quadrate zum heutigen Sudoku und dem steigenden Interesse in Japan. Der dritte und abschließende Teil der Sudokugeschichte betrachtet die Entwicklungen der letzten Jahre sowie die steigende Popularität.

Hier finden Sie eine Anleitung zum Lösen von Sudokus

Vor wenigen Jahren gab es einen regelrechten Boom und der Rätselspaß aus den USA war omnipräsent: In der S-Bahn, im Wartezimmer oder auf langweiligen Familienfeiern füllten Jung und Alt diese magischen Kästchen aus; der Süchtigmacher begeisterte die ganze Familie und ist auch heute noch ein gern gesehender Begleiter. Sudoku lernen macht einfach Spaß!

Doch worum geht es überhaupt? Wie sind die Sudoku Regeln? Ausgangspunkt ist ein großes Viereck, das in 9 kleine Vierecke unterteilt ist, welche wiederum jeweils in 9 Kästchen unterteilt sind. In jedem der Kästchen soll am Ende eine Zahl stehen - 1, 2, 3, 4, 5, 6, 7, 8 bis hin zur 9. Einige Zahlen sind zum Anfang des Spiels bereits vorgegeben; Ziel des Spiels ist es jetzt, alle freien Kästchen mit den Zahlen zu ergänzen. Die Schwierigkeit dabei: In jeder Reihe - horizontal wie vertikal - darf jede Zahl nur ein Mal erscheinen - noch dazu gilt genau diese Begrenzung für die 9 Vierecke, die sich aus dem großen Viereck bilden: Auch hier darf jede Zahl von 1-9 nur ein Mal vorkommen.

Das soll Spaß machen? Und wie! Was sich zunächst nach einem Hexenwerk anhört, versetzt einen relativ schnell in einen regelrechten "Flow", wenn man einer Sudoku Anleitung folgt: Ist man fast frustriert, weil man die nächste passende Lücke einfach nicht findet, hat man im nächsten Moment dann doch wieder das Erfolgserlebnis und macht weiter.

Eine Sudoku Spielanleitung kann darin bestehen, dass zunächst in alle freien Kästchen mit einem Bleistift hineinschreibt, welche Zahl dort hineingesetzt werden könnte - und diese dann nach Prüfung und Abgleich mit den anderen Reihen schrittweise wegradiert, bis nach dem ausschließenden Prinzip nur noch eine übrig bleibt, die dann zwingend eingesetzt werden muss.

Andere sehen als Sudoku Anleitung das bloße "ein Mal draufschauen und auf gut Glück einsetzen": Hier wird eher riskiert, statt klug taktiert; der Vorteil dieser Sudoku Anleitung kann sein, dass man schneller voran kommt - der große und zugleich frustrierende Nachteil kann sich aber daraus ergeben, dass man gegen Ende merkt, dass IRGENDWO etwas nicht ganz stimmt - und man dann ganz von neu anfangen müsste - bzw in der Praxis eher das nächste Sudoku beginnt und das bisherige als "nicht geschafft" durchstreicht und wegwirft.

Sudoku ist ein Spiel, dass in jedem Falle eine Anleitung benötigt. Gerade wenn man Sudoku das erste Mal in seinem Leben spielt wird man am Anfang des Spieles nur viele Zahlen unf hyroglyphen sehen, die erstmal keinen Sinn machen. Eine Sudoku Anleitung ist dabei so aufgebaut, dass sie Schritt für Schritt den Benutzer erklärt, wie Sudoku funktioniert. Dabei richtet man sich in aller erster Linie nach den Regeln, welche vor rund 21 Jahren in den USA auftraten. Sicherlich entstand Sudoku schon im Japan, wobei man festhalten muss, dass es in den USA erst publik und attraktiv in Umlauf gebracht worden ist. Eine Sudoku Hilfe hat also den Sinn, das Spiel auf bestmögliche Art und Weise zu erklären.

Sudoku funktioniert auf rein mathematischer Basis. Nehmen wir als Beispiel ein Feld mit der Größe 9 x 9. Dieses Feld besteht insgesamt aus einem großen Quadrat, das sich in neun weitere Quadrate unterteilen lässt. Jedes einzelne unterteilte Quadrat beinhaltet neun verschiedene Ziffern von 1-9. Die Problematik bei Sudoku besteht darin, dass jede einzelne Zahl von 1-9 nur einmal vorkommen darf und von Anfang an in jedem dieser Quadrate nur wenige Zahlen freigelegt sind. Die Aufgabe bei Sudoku liegt also darin, dass sie die restlichen Zahlen finden müssen und den jeweiligen Kästchen zuordnen müssen. Aufgrund der Tatsache, dass die gegenseitigen Quadrate zahlentechnisch abhängig zueinander sind, können sie immer nur eine bestimmte Zahl einem bestimmten Gitterraster zuordnen. Aus diesem Grund haben sie aus mathematischer Hinsicht immer nur einen einzigen Lösungsweg, der sich mit der richtigen Denkweise aber schnell finden lässt.

Mit den passenden Sudoku Tipps werden Ihnen viele Lösungsmöglichkeiten angeboten, über die sie ein Sudoku Rätsel leichter und schneller lösen können. Eine Sudoku Anleitung sollte sich immer nach dem jeweiligen Sudokuspiel orientieren. Wenn sie beispielsweise Killer Sudoku, Buchstaben Sudoku oder Samurai Sudoku spielen, benötigen Sie auch eine Sudoku Anleitung, die auf die einzelnen Regelungenmöglichkeiten genau eingehen kann.

Sudoku ist ein Spiel, dass in jedem Falle eine Anleitung benötigt. Gerade wenn man Sudoku das erste Mal in seinem Leben spielt wird man am Anfang des Spieles nur viele Zahlen unf hyroglyphen sehen, die erstmal keinen Sinn machen. Eine Sudoku Anleitung ist dabei so aufgebaut, dass sie Schritt für Schritt den Benutzer erklärt, wie Sudoku funktioniert. Dabei richtet man sich in aller erster Linie nach den Regeln, welche vor rund 21 Jahren in den USA auftraten. Sicherlich entstand Sudoku schon im Japan, wobei man festhalten muss, dass es in den USA erst publik und attraktiv in Umlauf gebracht worden ist. Eine Sudoku Anleitung hat also den Sinn, das Spiel auf bestmögliche Art und Weise zu erklären.

Sudoku funktioniert auf rein mathematischer Basis. Nehmen wir als Beispiel ein Feld mit der Größe 9 x 9. Dieses Feld besteht insgesamt aus einem großen Quadrat, das sich in neun weitere Quadrate unterteilen lässt. Jedes einzelne unterteilte Quadrat beinhaltet neun verschiedene Ziffern von 1-9. Die Problematik bei Sudoku besteht darin, dass jede einzelne Zahl von 1-9 nur einmal vorkommen darf und von Anfang an in jedem dieser Quadrate nur wenige Zahlen freigelegt sind. Die Aufgabe bei Sudoku liegt also darin, dass sie die restlichen Zahlen finden müssen und den jeweiligen Kästchen zuordnen müssen. Aufgrund der Tatsache, dass die gegenseitigen Quadrate zahlentechnisch abhängig zueinander sind, können sie immer nur eine bestimmte Zahl einem bestimmten Gitterraster zuordnen. Aus diesem Grund haben sie aus mathematischer Hinsicht immer nur einen einzigen Lösungsweg, der sich mit der richtigen Denkweise aber schnell finden lässt.

Mit der passenden Sudoku Anleitung oder Sudoku Strategien werden Ihnen viele Lösungsmöglichkeiten angeboten, über die sie ein Sudoku Rätsel leichter und schneller lösen können. Eine Sudoku Anleitung sollte sich immer nach dem jeweiligen Sudokuspiel orientieren. Wenn sie beispielsweise Killer Sudoku, Buchstaben Sudoku oder Samurai Sudoku spielen, benötigen Sie auch eine Sudoku Anleitung, die auf die einzelnen Regelungenmöglichkeiten genau eingehen kann.

Teil 1: Die magischen Quadrate

Im Normalfall gibt es nur eine einzige richtige Lösung für ein Sudoku. Allerdings gibt es sehr viele Wege, die zu dieser Lösung führen. Wir möchten hier verschiedene Varianten vorstellen, die zum Erfolg und einem gelösten Sudoku führen können. Nach dem Lösen einiger Rätsel hat man sich eine eigene Vorgehensweise angeeignet und verwendet dann diese.

Bei allen Vorgehensweisen steht die Grundregel eines jeden Sudokus im Mittelpunkt: In jeder Reihe, Spalte und jedem 3-mal-3-Unterquadrat dürfen die Zahlen 1 bis 9 nur genau ein mal vorkommen.Wenn Sie diese Regel beachten und Zahlen erst dann in ein Feld schreiben, wenn Sie sicher sind, dass keine andere Zahl in das Feld eingetragen werden kann werden Sie schnell auch schwierigste Sudokus lösen können.

Sehen wir uns nun 3 Lösungmöglichkeiten für Sudokus an, die mit Sicherheit zum Erfolg führen:

1. Lösungsmöglichkeit: Reihen, Spalten und Felder ausschließen

In jeder Spalte und Reihe eines Sudokus dürfen die einzelnen Zahlen nur genau ein mal vorkommen. Suchen Sie also nun in einem Unterquadrat die Position für eine fehlende 3, so untersuchen Sie die zugehörigen Reihen und Spalten ob bereits andere 3en eingetragen sind. Treffen Sie beispielsweise auf zwei Reihen in denen eine 3 eingetragen ist, so muss die 3 in Ihrem Unterqudrat in der 3. Reihe sein. Mit dieser Methode lassen sich nach und nach immer mehr Felder ausschließen und mit etwas Fleiß findet man das richtige Feld für seine Zahl.

2. Lösungsmöglichkeit: Reihen und Spalten ergänzen

Ist eine Reihe oder Spalte bereits mit vielen Zahlen gefüllt, so macht es meist Sinn zu versuchen die fehlenden Zahlen in diese Reihe oder Spalte einzufügen. Dabei muss die Sudoku-Grundregel beachtet werden. Wenn Sie in dieser Lösungsmöglichkeit die erste Variante anwenden, kommen Sie Schritt für Schritt auf die richtige Lösung.

3. Lösungsmöglichkeit: mögliche Zahlen notieren

Die letzte ist zwar die anstregendste Möglichkeit, sie trainiert jedoch Ihren Blick für die richtige Zahl. Kommt man einfach nicht weiter beim Lösen eines Sudokus, kann es helfen sich für jedes freie Feld die möglichen Zahlen klein in das Feld zu schreiben. Das schafft einen guten Überblick. Je länger Sie spielen um so leichter ist es, die möglichen Zahlen einfach im Kopf zu behalten.

Beispiel-Sudoku mit Lösung

Abbildung 1 zeigt ein einfaches Sudoku für den Einstieg, welches wir Schritt für Schritt lösen werden. Beachten Sie dabei, dass der vorgestellte Lösungsweg nur einer von vielen ist. Zu jeder Zeit können Sie auch eine andere Zahl zuerst finden. Suchen Sie zunächst nach Reihen und Spalten in denen eine Zahl mehrfach vorkommt.

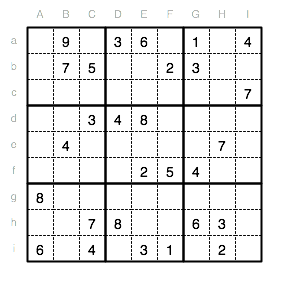
In Spalte I und G kommt beispielsweise eine 4 vor. Im Unterquadrat IX hingegen fehlt die 4 noch. Die 4 in diesem Unterquadrat darf nicht in den Spalten I und G sein. Also darf die 4 nur im Feld Hg eingetragen werden.

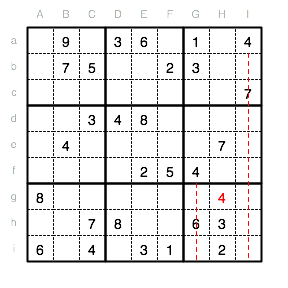
Im nächsten Schritt muss in Reihe g eine 3 eingetragen werden. Da in den Unterquadraten VIII und IX bereits 3en eingetragen sind, muss die 3 im Quadrat VII in Reihe g. Da in Spalte C bereits eine 3 steht, muss die fehlende 3 also in Bg eingetragen werden.

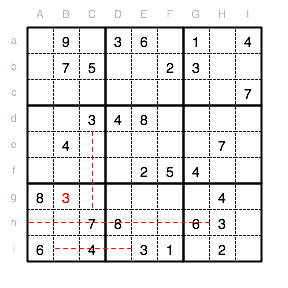
Das gleiche Vorgehen gilt auch für die 3 im Feld Ac.

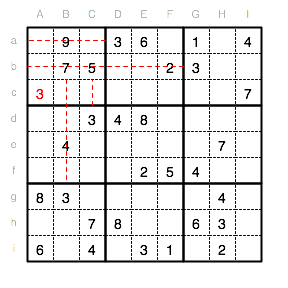
In Spalte F fehlt eine 3. Da diese nicht in Unterquadrat II und VIII sein kann, muss sie in Unterquadrat V sein. In Reihe d steht schon eine 3, also muss die fehlende 3 in das Feld Fe.

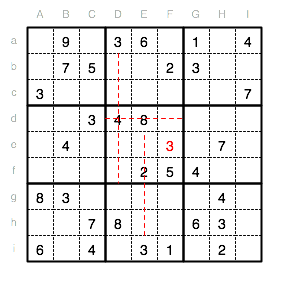
Nun fehlt nur noch im Unterquadrat VI eine 3. In den Reihen d und e stehen bereits 3en. Auch in den Spalten G und H sind diese schon eingetragen. Als einzige Möglichkeit bleibt also das Feld If.

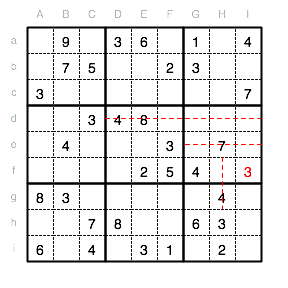
Wenn wir nun nach der nächsten Ziffer suchen, so stoßen wir im Unterquadrat VIII auf eine fehlende 2. Diese kann nicht in Spalte E oder F stehen und auch nicht in Reihe i. Es bleibt als Position also nur Dg.

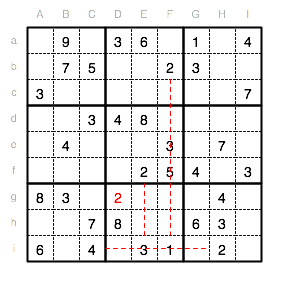
Das gleiche Vorgehen gilt auch für die Suche der Position für die 7 im Unterquadrat II.

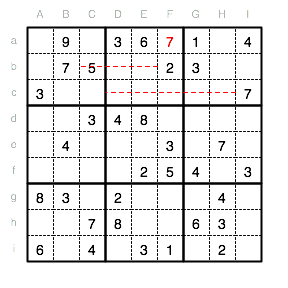
Im Unterquadrat III kann eine 2 nur in das Feld Gc eingetragen werden, da die Spalte H und die Reihe c bereits eine 2 enthalten.

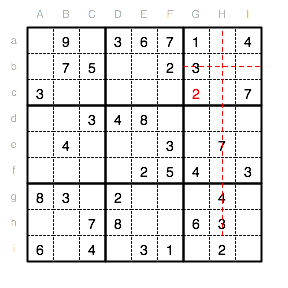
In der Reihe a muss eine 5 eingetragen werden. Als mögliche Positionen sind noch Aa, Ca und Ha verfügbar. Da jedoch im Unterquadrat I bereits eine 5 steht, fallen Aa und Ca als Positionen weg und es bleibt nur noch Ha als Position für eine 5.

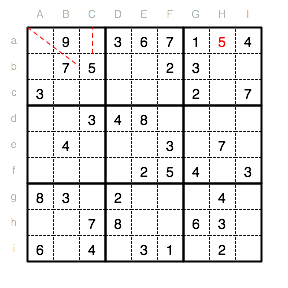
Nun fehlen noch eine 8 und eine 2 in Reihe a. Da in Spalte A bereits eine 8 steht, muss die 8 in Reihe a also in Ca.

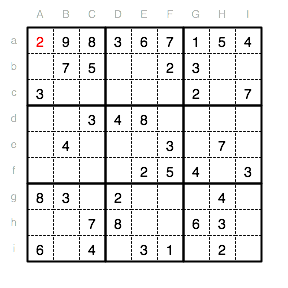
Als einzige Position für die 2 bleibt also das Feld Aa. Wir haben jetzt die erste komplette Reihe und nähern uns dem Ende.

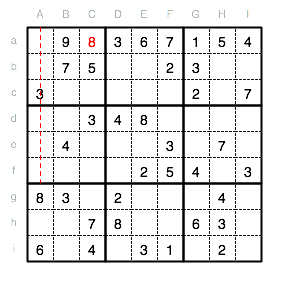
Die Spalten B und C enthalten bereits 4en. In Spalte A und Unterquadrat I fehlt die 4 noch und als Position ergibt sich nur das Feld Ab.

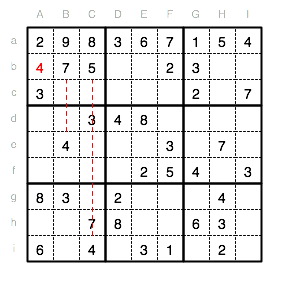
Durch die 2, die wir in Schritt 11 geschenkt bekommen haben, können wir nun im Unterquadrat VII eine 2 eintragen. Die Spalte A sowie die Reihen g und i scheiden als mögliche Positionen aus. Es bleibt das Feld Bh.

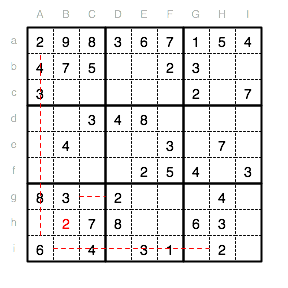
Für eine 7 im Unterquadrat V kommt nur die Position Df in Frage, da die Reihe e und die Spalte F bereits 7en gesetzt haben.

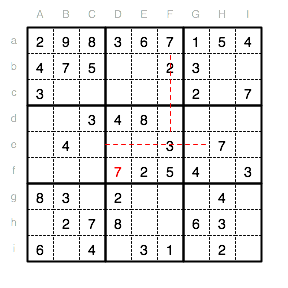
Mit der soeben eingetragenen 7 in Df können wir nun auch in Reihe d eine 7 setzen. Die Reihen e und f scheiden aus, genau wie die Spalte B. Es bleibt also nur das Feld Ad.

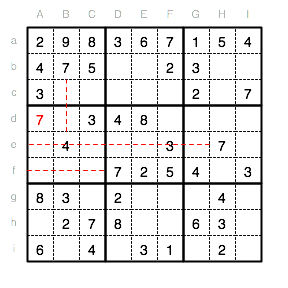
Die Unterquadrate VIII und IX haben noch keine 7 gesetzt. Da die Spalten D und F bereits eine 7 haben und auch die Reihe h können wir für das Unterquadrat VIII das Feld Eg als Position feststellen.

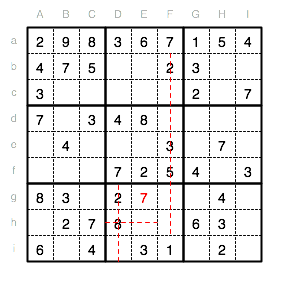
Für das Unterquadrat IX bleibt dann nur noch Gi als Position für die 7.

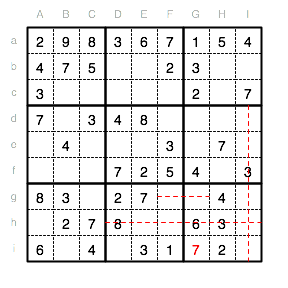
Das Ausschlußverfahren können wir nun auch bei der 6 im Unterquadrat XIII anwenden. Als Position bleibt schließlich nur Fg.

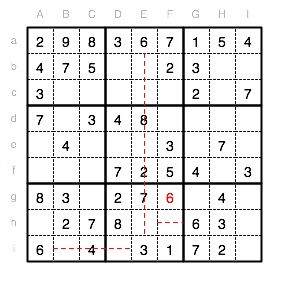
Bedenken Sie bei der Lösung, dass Sie jederzeit einen anderen Lösungsweg nehmen können als wir. Am Ende werden Sie -- wenn Sie alles richtig gemacht haben -- zum gleichen Ergebnis kommen. Wir betrachten im nächsten Schritt die Spalte G und stellen das Fehlen einer 8 fest. Ausschleißen können wir jedoch wieder die Reihen d und g. Es bleibt also nur das Feld Ge für die 8. Sehen Sie, wie einfach Sudoku ist?

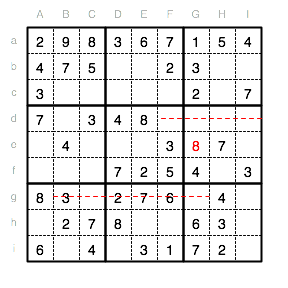
Die nächste 8 muss in das Feld Ii gesetzt werden, da die Reihen g und h bereits eine 8 besitzen und somit nur Ii im Unterquadrat IX als Möglichkeit bleibt.

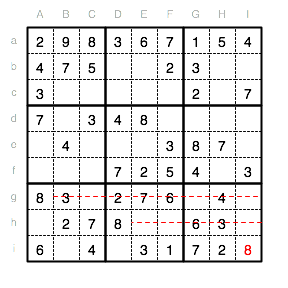
Und weiter geht es mit den 8en in diesem Sudoku-Rätsel. In Spalte B muss eine 8 gesetzt werden. Da im Unterquadrat I bereits eine 8 ist, fällt Bc als Position weg. Die Reihen d und i haben ebenfalls bereits eine 8 also muss die fehlende 8 in Bf eingetragen werden.

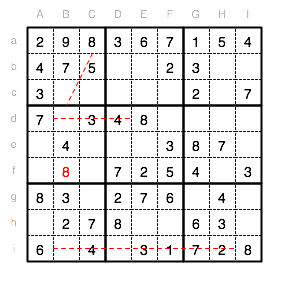
Auch im Unterquadrat II fehlt eine 8, welche nur in Spalte F gesetzt werden kann. Das einzig freie Feld ist Fc. Also muss die fehlende 8 genau dort eingetragen werden.

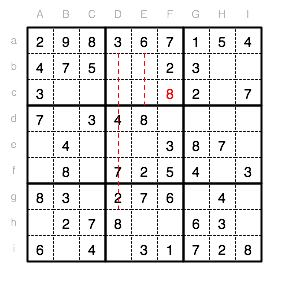
Bleiben wir in diesem Unterquadrat, so fehlt hier auch eine 4. Diese kann nicht in Spalte D oder in Reihe b stehen. Es bleibt also nur das Feld Ec.

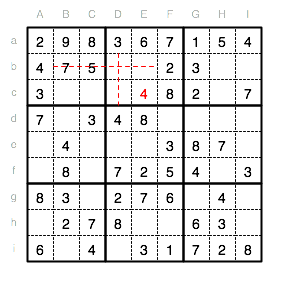
Auch für die 5 gibt es in diesem Unterquadrat nur eine Position, da sie nicht in Reihe b stehen kann. Die 5 muss also in Dc eingetragen werden.

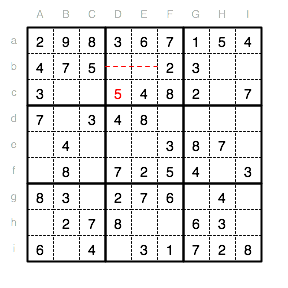
Durch die Eintragung kann die 5 in Reihe i nur noch im Feld Bi stehen.

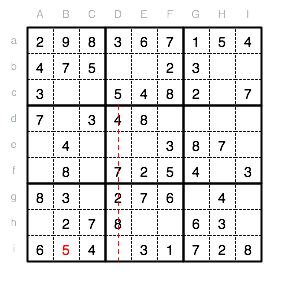
Nun fehlt in Reihe i nur noch eine 9 und es gibt auch nur ein freies Feld. In Di kommt also eine 9. Wir haben nun unsere zweite vollständige Reihe und nähern uns mit großen Schritten dem Finale dieses Rätsels.

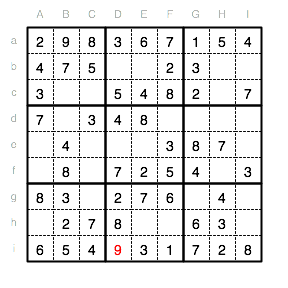
In Unterquadrat II gibt es nun nur noch eine Position für die 9 (Eb). Im nächsten Schritt vervollständigen wir das Unterquadrat mit der fehlenden 1 im Feld Db.

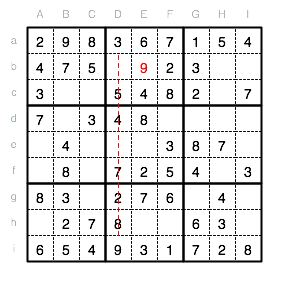
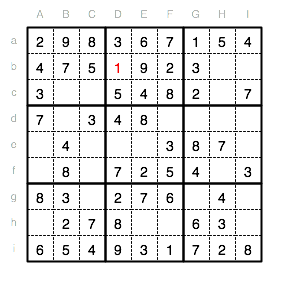
Auch im Unterquadrat III fehlt eine 9. Diese kann nur in Hc eingetragen werden, da die Reihe b bereits eine 9 enthält und sonst keine leeren Felder mehr vorhanden sind.

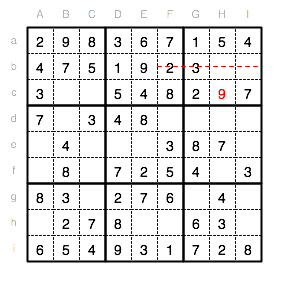
Auch für die 8 (Hb) und die 6 (Ib) gibt es in Reihe b und dem Unterquadrat III nur eine Möglichkeit. Ab jetzt wird es immer einfacher das Rätsel zu beenden.

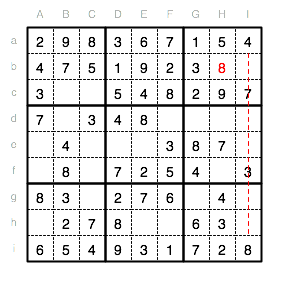
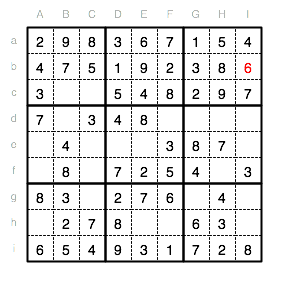
Das Unterquadrat V und die Spalte F benötigen noch eine 9. Als einzige Position ergibt sich offensichtlich Fd.

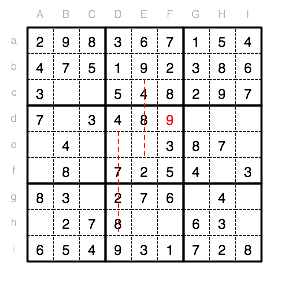
Nun fehlt in Spalte F als letzte Ziffer eine 4. Das einzig freie Feld ist Fh. Auch die Kontrolle ergibt, dass die 4 dort genau richtig ist.

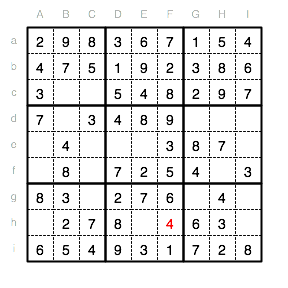
Im Unterquadrat V fehlen nun noch die Ziffern 1 und 6. Für die 1 bleibt nur Ee als mögliches Feld.

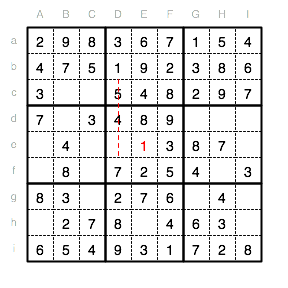
Dadurch muss die 6 dann im Feld De eingetragen werden.

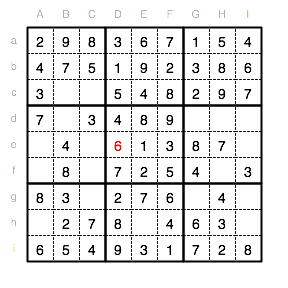
Betrachten wir die Spalte G: Es fehlen die Ziffern 9 und 5. Im Moment kann für die 5 nict gesagt werden, ob sie in Gd oder Gg eingetragen werden muss. Für die 9 lässt sich hingegen feststellen, dass die Reihe d ausscheidet. Die 9 muss also in das Feld Gg eingetragen werden.

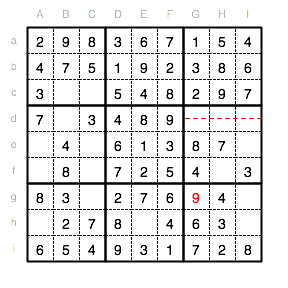
Für die 5 bleibt demzufolge nur noch das Feld Gd.

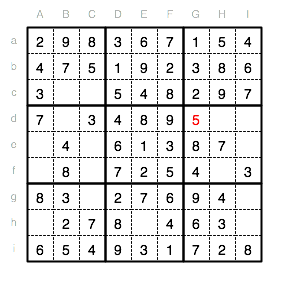
Das Eintragen der letzten 5 ermöglicht es uns im Unterquadrat IV eine 5 zu setzen. Die Spalte C scheidet aus, auch in den Reihen d und f stehen bereits 5en. Es bleibt also wieder nur eine Position: Ae.

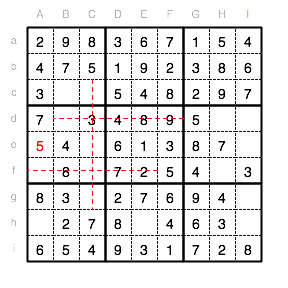
Im Unterquadrat VI kann die 9 nur in Ie stehen.

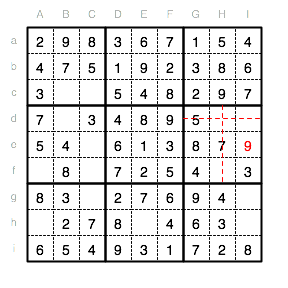
Jetzt kann die letzte fehlende Zahl in die Reihe e eingetragen werden. Die 2 kommt in Ce.

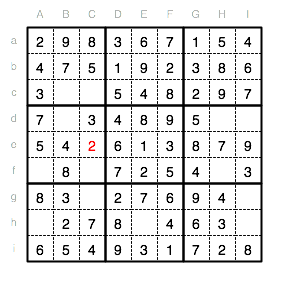
In der Spalte I fehlt jetzt noch eine 2. Diese kann nur in Id stehen.

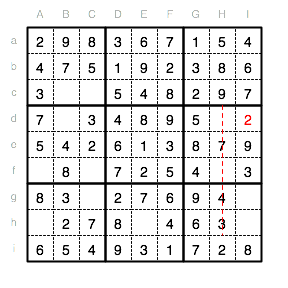
Nun vervollständigen wir das Unterquadrat VIII mit der fehlenden 5 an Position Eh.

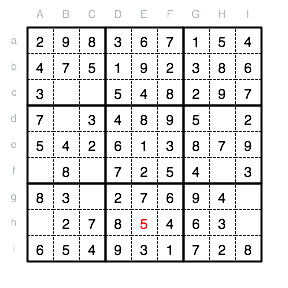
Aus dieser Eintragung können wir schließen, dass auch im Feld Ig eine 5 stehen muss. Das Unterquadrat IX muss dann noch mit einer 1 aufgefüllt werden.

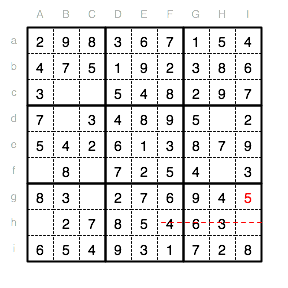
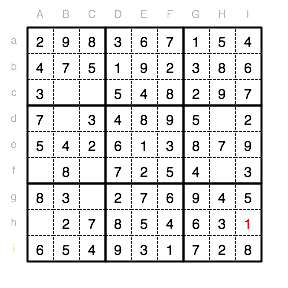
Im Endspurt des Rätsel können wir nun in Reihe G die fehlende 1 im Feld Cg eintragen.

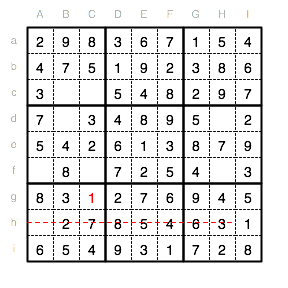
Von dieser 1 ausgehend muss also auch in Bc eine 1 stehen.

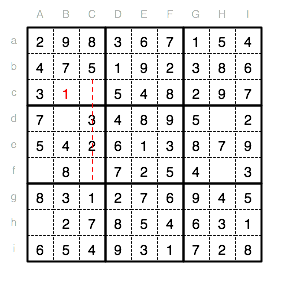
Die letzte fehlende Ziffer im Unterquadrat I ist eine 6. Wir tragen diese im letzten freien Feld Cc ein.

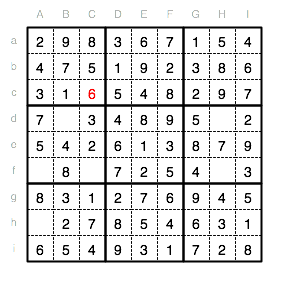
Nun suchen wir im Unterquadrat IV nach einer Position für die fehlende 1. Einzig Spalte A und Feld Af bleiben als Mšglichkeit fŸr diese 1.

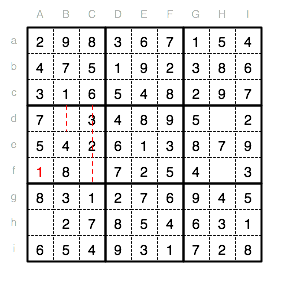
Das Sudoku zu beenden ist nun nur noch reine Fleißarbeit. Im Unterquadrat VI kann die 1 nur an Position Hd eingetragen werden.

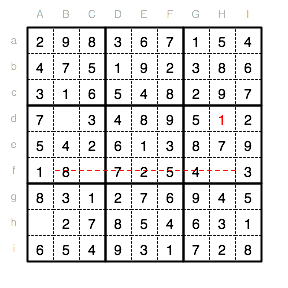
Die letzte noch fehlende Ziffer ist die 6, welche ins Feld Hf gesetzt wird.

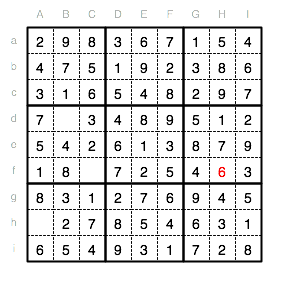
Nun können wir die Reihe f mit einer 9 an Position Cf vervollständigen.

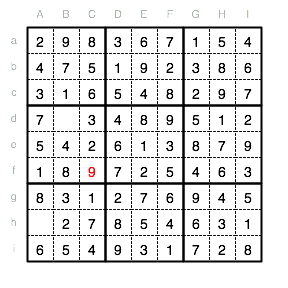
Der Spalte B fehlt nur noch eine 6 im Feld Bd.

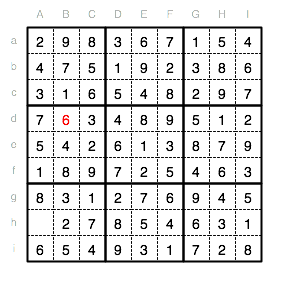
Die letzte Ziffer des Sudoku-Rätsels ist eine 9 im Feld Ah.

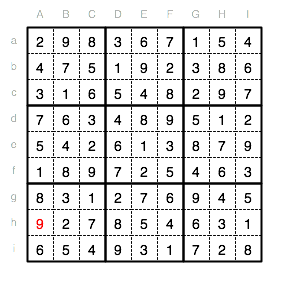
Fazit

Wie Sie sehen, ist es sehr einfach Sudokus zu lösen. Sie müssen nur aufmerksam die bereits eingetragenen Ziffern beobachten und sich überlegen an welcher Position welche Ziffer eingetragen werden kann. Beachten Sie die Grundregel, dass in jeder Reihe, Spalte und jedem 3-mal-3-Unterquadrat die Zahlen 1 bis 9 nur genau ein mal vorkommen dürfen und Sie werden zum Sudoku-Meister.